Panoramy zawsze znajdowały swoje miejsce w przedstawianiu rzeczywistości. Pojawiały się już w malarstwie, pozwalając na pełniejsze prezentowanie miejsc bądź wydarzeń. W czasach fotografii, gdy ich tworzenie jest łatwiejsze, trudno nie docenić możliwości ukazania fotografowanego miejsca inaczej niż za pomocą pojedynczego kadru. Z początku pod pojęciem panoram rozumieliśmy głównie sklejanie kilku zdjęć, wykonanych w poziomie i pionie.

Prosta panorama

Panorama taka jest jednak de facto jedynie kolejną fotografią, z szerszym kątem widzenia fotografowanej sceny. Rozpowszechnienie Internetu, a w raz z nim interaktywnych form prezentacji, sprawiło natomiast, że łatwiejsze stało się nadanie panoramom nowego wymiaru – interaktywności. Nie musimy być już biernym widzem, możemy zanurzyć się w prezentowanej panoramie i rozglądać dookoła.

Idea wykonywania tego typu panoram jest prosta – musimy wykonać kilka (kilkanaście) zdjęć, fotografując otoczenie wokół siebie. Następnie zdjęcia te odpowiednio ze sobą łączymy przy pomocy specjalnego programu komputerowego.

----- R E K L A M A -----

ZIMOWY CASHBACK OD CANONA 2024/25

Canon 85/2 RF Macro IS STM

2598 zł 2398 zł

Canon 70-200/4 RF L IS USM

6996 zł 6496 zł

Canon R8 (EOS R8) + 24-50/4.5-6.3 RF ...

6493 zł 5993 zł

Canon R6 Mark II + 24-105/4 RF L

15498 zł 14498 zł

W zależności od tego jak wykonamy zdjęcia, utworzyć możemy dwa główne typy panoram:

• cylindryczna (dookólna) – możemy rozglądać się jedynie na boki. Sytuację taką przedstawia poniższy rysunek.

Panorama cylindryczna

• sferyczna (kulista) – pozwala rozglądać się na wszystkie strony, również do góry oraz na dół. Schemat tego typu przedstawia poniższy rysunek.

Panorama sferyczna

Ciekawszy w odbiorze efekt tworzy oczywiście ten drugi typ panoram, pierwszy jest natomiast trochę prostszy do uzyskania. W poradniku tym zajmiemy się tworzeniem panoram sferycznych. Nie jest to zagadnienie tak skomplikowane jak mogłoby się wydawać, a ewentualny trud szybko rekompensowany jest ciekawymi efektami.

Pamiątka w postaci interaktywnej panoramy miejsca, w którym byliśmy jest czymś innym niż zwykłe fotografie. Nie musimy rozważać kadru, zastanawiać się, które szczegóły chcemy ukazać, a które ukryć. Kadr jest wszędzie dookoła nas, więc klasyczne metody kompozycji tracą na znaczeniu. Nie oznacza to oczywiście, że wystarczy wykonać panoramę w dowolnym, przypadkowym miejscu, by uzyskać ciekawy efekt. Jedne zasady kompozycji zastąpić możemy w tym przypadku innymi, które określić można mianem „przestrzennych”. W poradniku tym przedstawiamy więc zarówno technikę wykonywania panoram jak i kilka nowych porad kompozycyjnych, na które warto zwracać uwagę przy ich tworzeniu.

Temat tworzenia panoram sferycznych poznawać będziemy stopniowo, stosując coraz bardziej zaawansowane techniki, a ewentualne porażki doświadczone po drodze pozwolą zrozumieć jakie metody i sprzęt są do takich zadań najdogodniejsze. Zanim jednak przejdziemy do praktyki, poznać będziemy musieli trochę teorii, bez której trudno zrozumieć to zagadnienie.

Trochę teorii

Aby stworzyć poprawną panoramę, musimy wykonać serię zdjęć w różnych kierunkach, tak jak na rysunku powyżej. Następnie musimy takie zdjęcia ze sobą połączyć – automatycznie bądź ręcznie. Połączenie to ma na celu stwierdzenie jak zorientowane były względem siebie kadry. Odbywa się to za pomocą tzw. punktów wspólnych (kontrolnych) – czyli fragmentów kadru wspólnych dla różnych zdjęć.

Przykładowe punkty wspólne pomiędzy dwoma kadrami

Oczywiste staje się zatem, że kolejne zdjęcia muszą być tak wykonywane, by owe części wspólne posiadały. Tak zwana „zakładka” powinna występować pomiędzy każdą parą sąsiadujących ze sobą zdjęć i wynosić około 20–30% odpowiednich brzegów kadru. Zapewni to, że na zakładce znajdzie się odpowiednia ilość charakterystycznych, możliwych do rozróżnienia punktów wspólnych. Nietrudno się bowiem domyślić, że np. jednolite niebo nie jest dobrym kandydatem do poszukiwań takich punktów.

Inną kwestią jest to, by poszczególne fotografie dało się na siebie poprawnie nałożyć. Podstawowym problemem pod tym względem jest tzw. błąd paralaksy. Paralaksa ma kilka definicji, jednak na potrzeby tego artykułu powiedzieć można, że jest to zjawisko, które oznacza niepokrywanie się obrazów obserwowanych z różnych punktów widzenia. Bardzo łatwo się o tym przekonać za pomocą naszych własnych oczu. Jeżeli wyciągniemy przed siebie rękę, to patrząc na nią lewym okiem widzieć będziemy za nią inne tło, niż gdy popatrzymy prawym okiem. Na rękę i tło patrzymy bowiem z różnych, przesuniętych względem siebie punktów widzenia.

Dwa zdjęcia z widocznym błędem paralaksy

Błąd paralaksy jest problematyczny, ponieważ wykonując zdjęcia nim obarczone, nie będziemy w stanie dopasować ich do siebie. Spójrzmy na próbę nałożenia na siebie dwóch zdjęć z widocznym błędem paralaksy:

Nieudana próba połączenia zdjęć z błędem paralaksy

Choć zdjęcia mają „zakładkę”, to nie da się ich poprawnie połączyć, ponieważ obiekt z pierwszego planu zasłania na nich inną część tła.

Z pomocą przychodzi nam w tym momencie teoria, w której istnieje pojęcie punktu bez błędu paralaksy (ang. NPP – No Parallax Point). Punkt NPP jest punktem, wokół którego obracając układ obiektyw-aparat i wykonując zdjęcia, nie będziemy uzyskiwać błędu paralaksy. Innymi słowy, niezależnie jak obrócimy aparat wokół punktu NPP, obiekty z pierwszego planu będą zasłaniać drugi plan w dokładnie taki sam sposób.

Dwa zdjęcia bez widocznego błędu paralaksy

Sytuacja taka sprawia, że kolejne zdjęcia można na siebie idealnie nakładać, ponieważ nie występują rozbieżności pomiędzy pierwszym i drugim planem na poszczególnych zdjęciach.

Udana próba połączenia zdjęć bez błędu paralaksy

Z powyższych rozważań wysnuć można ważny wniosek – błąd paralaksy jest tym istotniejszy, im bliżej aparatu umieszczone są obiekty na pierwszym planie. Im bowiem większa odległość, tym różnice w zarejestrowanych obrazach będą mniejsze. Dlatego fotografując np. górską panoramę, w której pierwszy plan praktycznie nie występuje, błąd paralaksy będzie znacznie mniej dokuczliwy, niż w przypadku wykonywania panoramy np. własnego pokoju. Takie sytuacje występują jednak bardzo rzadko i dlatego lepiej jest fotografować zawsze starając się owego błędu uniknąć.

Położenie punkt NPP wyznacza konstrukcja danego obiektywu. Często nazywa się go w artykułach dotyczących panoram punktem węzłowym bądź nodalnym, chociaż jest to określenie błędne. Określenie to jest jednak tak często używane, że stało się nieomal synonimem poprawnej nazwy – punktu źrenicy wejściowej. Trudno powiedzieć czy fakt używania błędnej nazwy wynika z niezrozumienia znaczenia punktu nodalnego, czy też jest po prostu nadużyciem tej nazwy i nieświadomą próbą nadania mu innego znaczenia.

Tak czy inaczej, tworząc poradnik dotyczący panoram sferycznych nie sposób nie wykorzystać okazji by rozprawić się z tą błędną terminologią. Jeżeli jednak nie interesują Was teoretyczne podstawy związane z położeniem punktu NPP oraz jego poprawną nazwą, bez szkody dla zrozumienia całości pominąć możecie ten rozdział, przechodząc od razu do następującej po nim części praktycznej. Bardziej wnikliwych zachęcamy jednak do lektury, choćby po to, by móc w przyszłości wyprowadzać inne osoby z tego powszechnie powtarzanego błędu.

Przez punkt nodalny często rozumie się w poradnikach dotyczących panoram taki punkt, w którym „przecinają się w obiektywie promienie światła przed trafieniem na matrycę”. Obrazowane jest to często poniższym schematem.

Często spotykany schemat położenia „punktu nodalnego”

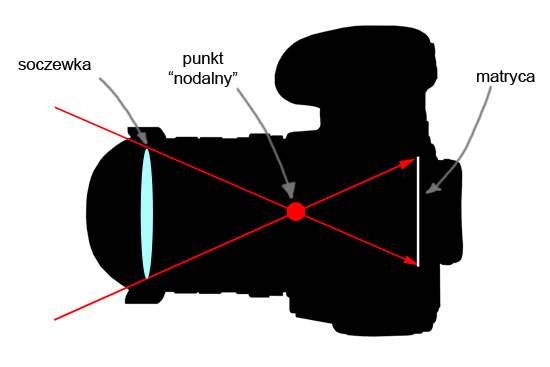Przy takiej definicji „punktu nodalnego”, staje się oczywiste, że aby uniknąć błędu paralaksy, należy obracać aparat właśnie wokół niego. Obrazy dwóch różnych punktów w przestrzeni nie przesuwają się w takiej sytuacji względem siebie.

Obrót wokół „punktu nodalnego”

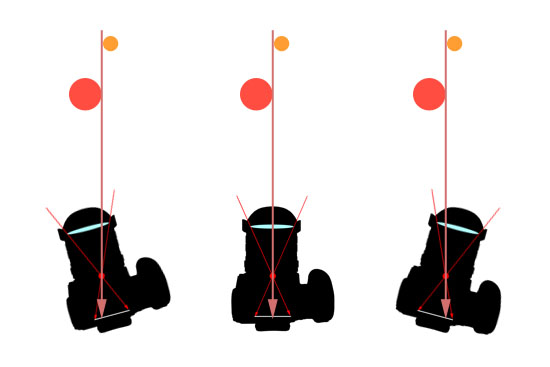Problem jednak w tym, że powyższe definicje mijają się z prawdą. Wynikają bowiem ze zbyt daleko idącego uproszczenia budowy obiektywu. W powyższych schematach traktowany jest on jako model pojedynczej, cienkiej soczewki i choć w wielu sytuacjach może być wystarczający, do tematyki błędu paralaksy się nie nadaje. Lepszym, bardziej adekwatnym modelem obiektywu jest tzw. model soczewki grubej. Uwzględnia on fakt, że obiektyw jest skomplikowanym układem optycznym składającym się z wielu soczewek o różnej wielkości i kształcie. Model jednak nie próbuje nawet „zgadywać” jak ten układ wygląda ani jak wędruje światło wewnątrz obiektywu. De facto zastępuje on cały obiektyw jedną, grubą soczewką wypukłą. Pozwala to w dobry sposób opisywać zachowanie światła na zewnątrz soczewki (obiektywu), dając jednocześnie wgląd w zachodzące przy tworzeniu obrazu zależności geometryczne.

Model obiektywu jako soczewka gruba

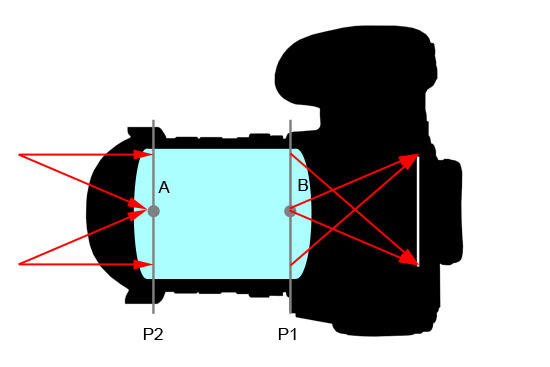W modelu tym występują wspomniane wcześniej punkty główne (A i B) – w miejscu przecięcia płaszczyzny głównej obrazowej (P1) i przedmiotowej (P2) z osią optyczną obiektywu. Obracanie aparatu wokół nich niewiele ma jednak wspólnego z niewystępowaniem błędu paralaksy. Czasem uważa się też, że obiektyw powinno obracać się wokół punktu wyznaczonego przez położenie przysłony – może to ona jest owym miejscem, w którym „przecinają się w obiektywie promienie światła przed trafieniem na matrycę”? Choć powoli zbliżamy się do prawdy, wciąż nie jest to poprawne położenie. Punktem bez błędu paralaksy jest bowiem nie środek samej przysłony, lecz jej obrazu widzianego przez przednią soczewkę – tzw. źrenicy wejściowej. Jej położenie niewiele ma wspólnego z położeniem punktów nodalnych, a jego wizualnej ocenie przyjrzymy się jeszcze w dalszej części artykułu.

Niestety klarowne wytłumaczenie czemu to właśnie pozycja źrenicy wejściowej jest poprawnym punktem NPP wykracza poza ramy tego poradnika. Możemy sobie to jednak próbować wytłumaczyć w sposób intuicyjny – źrenica wejściowa jest otworem, który widzimy patrząc na obiektyw z przodu i to przez nią światło dociera przez obiektyw do matrycy. Odwracając więc sytuację – to przez nią matryca „widzi” świat. Chcąc uniknąć błędu paralaksy to właśnie poruszania tego punktu powinniśmy więc uniknąć.

Po zaznajomieniu z pewną dawką teorii, przejść możemy do bardziej praktycznych rozważań, dotyczących zarówno techniki jak i używanego sprzętu.